Nå hadde jeg egentlig tenkt å skrive om elementærpartikler, men så oppdaget jeg at jeg har berørt temaet før, i langt mer detalj enn jeg hadde tenkt å gjøre denne gangen. Jeg skrev nemlig om
elementærpartikler i oktober i fjor. Den gangen sa jeg følgende:
Men vi slutter ikke der, vi har enda flere elementærpartikler, nemlig de kraftbærende partiklene. Den første er fotonet, som burde være velkjent. Det som kanskje ikke er velkjent er at fotonet er den partikkelen som overfører elektriske og magnetiske krefter. I tillegg har vi gluonet, som overfører den sterke kraften (den som holder positive protoner sammen i atomkjernene), og W og Z, som har med den svake kraften å gjøre. W finnes i to utgaver, en positiv og en negativ, så da har vi 5 kraftbærende partikler. Noen savner kanskje gravitonet, men det er ikke en del av Sannheten™.Derfor skal jeg heller snakke om gravitasjon i dag. Den kjente og kjære måten å tenke på gravitasjon er den vi lærer i ex.phil., med Newton og eplet. Gravitasjonskraften er proporsjonal med massen, og omvendt proporsjonal med kvadratet på avstanden. Ferdig arbeid. Så hva skjer hvis Sola plutselig forsvinner, vil vi oppdage det sånn gravitasjonsmessig med en gang, eller 8 minutter senere, samtidig som lyset går? La oss ikke tenke på det. Men så hva skjer i et sort hull, skjer det noe spesielt der? Nei, la oss ikke tenke på det heller. Ok, men hva med presesjon av gyroskoper i nærvær av en roterende masse? Hva, hæ, sa du?
Poenget mitt er at Newtons gravitasjon, akkurat som Newtons lover, fungerer helt ok for de fleste, men ikke for de tøffeste fysikerne, som regner på de tyngste tingene, og de raskeste partiklene. Einsteins generelle relativitetsteori er essensielt en teori for gravitasjon, der man ikke snakker om en kraft som vekselvirker mellom to masser, men heller at en masse krummer rommet rundt seg. Når jeg sier krumme mener jeg naturligvis på en skikkelig anti-intuitiv måte. Jeg sliter for eksempel med å tegne en firedimensjonal hyperboloide i et femdimensjonalt rom.
Måten gravitasjonen kommer til uttrykk på, er at når masser beveger seg langs rette linjer i et krummet rom ser det for oss ut som om de beveger seg i krumme linjer. Ganske funky. Men det som er virkelig funky er at rommets krumming også påvirker tiden, slik at tiden går langsommere i et kraftigere gravitasjonsfelt. For å beskrive det krummede rommet bruker man noe som kalles en metrikk, som egentlig er en avstandsfunksjon. Schwarzchildmetrikken, for eksempel, ser slik ut
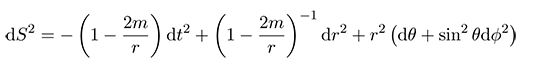
Denne metrikken beskriver rommet utenfor et sort hull. Vi ser straks at her skjer det noe funky når r=2m. Hva skjer? Det kan du få lov til å tenke litt på, hvis du liker denslags. Men jeg kan i allefall nevne at r=2m er den tidligere omtalte Schwarzchildradiusen, eller hendelseshorisonten, som ingenting kan slippe ut fra.
Generell relativitet er altså den rådende måten å beskrive gravitasjon på i dag, hvis man trenger en mer cutting-edge formulering enn den du finner i Dybvig og Dybvig. Den har blitt testet i alle retninger, og har holdt seg bra så langt. Disse testene skal jeg fortelle deg mer om senere. I morgen: Kvantegravitasjon.
-Tor Nordam

Comments