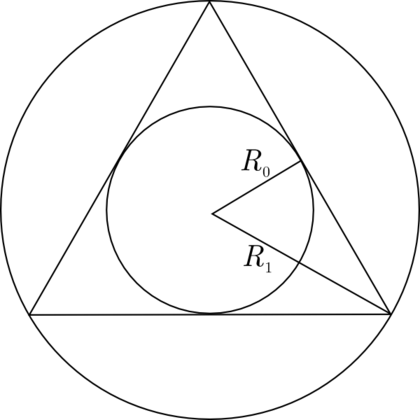
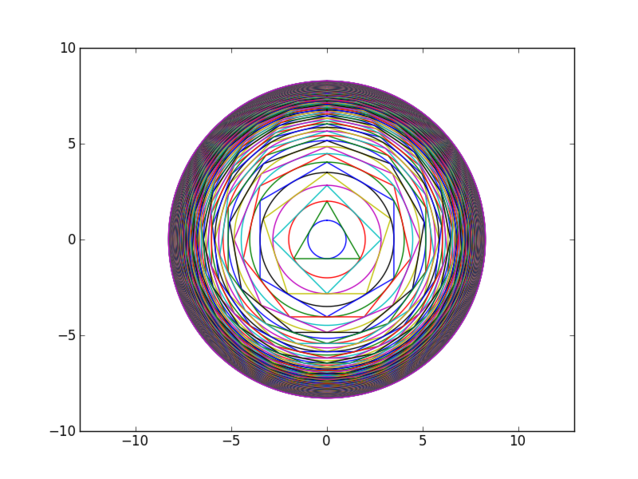
Jørgen ringte i går, og lurte på om jeg hadde noen tanker om en matteoppgave han hadde sett på. Oppgaven går som følger: Man begynner med en sirkel. Så tegner man en likesidet trekant som omskriver sirkelen, og en ny sirkel som omskriver trekanten.
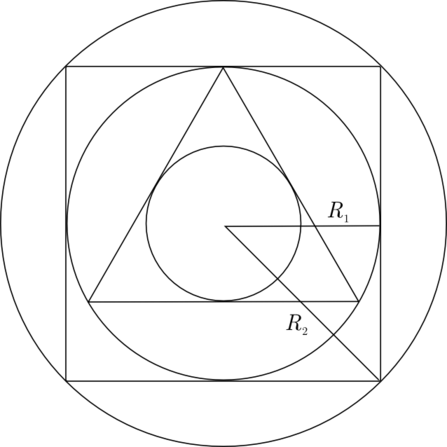
Man gjentar så prosessen med en firkant
og videre med en femkant, etc., etc. Hver nye sirkel vil være større enn den forrige, men radien vil øke mindre for hver gang, og oppgaven går ut på å vise at når antallet figurer går mot uendelig vil radien til den største sirkelen gå mot en grense. Her må vi altså ty til matematikk.
Hvis radien til den første sirkelen er
R0 vil radien til den andre sirkelen være
R1, der
og videre vil radien til den neste sirkelen være
og vi ser at radien vil gå mot
Det kan tenkes at dette kan skrives om til noe mer elegant, muligens ved hjelp av en eller annen frekk representasjon av cosinus som et uendelig produkt og en smart måte å sette sammen faktorer slik at man ser et slags mønster, men jeg har ikke greid det. Oppgaven gikk imidlertid ut på å finne det minste heltallet som er større enn grensen radien går mot, og hvis man er på en pubquiz eller noe, så holder det ikke å si at du har funnet svaret representert som et uendelig produkt. De vil ha et tall. Jeg prøvde å putte uttrykket inn i
Wolfram Alpha og regne ut produktet opp til et stort tall, men den sluttet å samarbeide før jeg kom til 10000, og selv om det sikkert er bra nok ville jeg ikke gi meg der, så jeg fant frem python.
Siden dette er et eksempel på en ting som er vanskelig å regne ut på papir, men lett å regne ut med bittelitt programmering, og siden Jørgen og jeg disukterte python sist jeg var i Oslo, tenkte jeg å vise hvordan man kan studere dette problemet. På Mac eller linux, åpne en terminal og skriv python. Da får du opp et interaktivt python shell som du kan bruke som en kalkulator.
For å studere dette problemet trenger vi først cosinus og pi, som vi kan importere fra math-modulen. Skriv
from math import cos, pi
Så skal vi definere en funksjon. Skriv
def f(N):
p = 1
for n in xrange(3,N):
p = p * 1 / cos( pi / n )
return p
Legg merke til at indenteringen er viktig i python. Nå har vi laget en funksjon som regner ut produktet vårt fra 3 og opp til
N. Dermed kan vi lettvint teste ulike verdier av
N og se om det ser ut til at vi nærmer oss en grense. Skriv for eksempel
f(1000)
og
f(10000)
og
f(100000)
og se hva som skjer. Det ser ut til at det minste heltallet som er større en grensen vi leter etter er 9, og når jeg beregnet det undelige produktet numerisk med Mathematica fikk jeg 8.7004, så vi ser at rekken har konvergert ganske fint allerede ved
N=100000.
Det er naturligvis juks & fanteri å løse en slik oppgave på denne måten, men det er likevel noe tilfredsstillende i å skrive noen få linjer kode og regne ut et produkt av hundre tusen eller en millon faktorer på et lite sekund, og se at svaret konvergererer fint.
-Tor Nordam

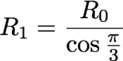
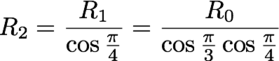

Comments