Fourier-analyse er en matematisk teknikk som går ut på å analysere et signal for finne ut hvilke frekvenser det består av, og det kan derfor også kalles frekvensanalyse. Som et eksempel kan vi begynne med å lytte til dette lydklippet:
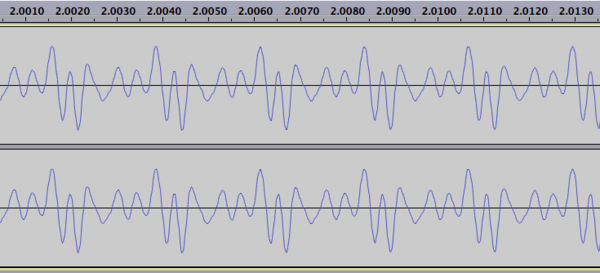
Det er en liten snutt med lyd fra en gitar som spiller en A. Hvis vi tar nærmere kikk på et lite utsnitt av lyden ser det slik ut:
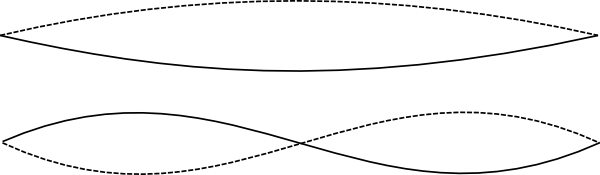
Vi ser at signalet stort sett varierer ganske jevnt. Den høye toppen man ser gjenta seg med omtrent 0.0022 sekunders mellomrom er grunnfrekvensen til gitarstrengen, som her er på 440 Hz. I tillegg ser vi at signalet har komponenter som varierer raskere. Dette er de såkalte overtonene til gitarstrengen, som skyldes at det finnes mer enn én måte strengen kan vibrere på, strengens såkalte egenmoder. Her har jeg forsøkt å illustrere de to første modene:
Den moden der hele strengen svinger frem og tilbake er grunnfrekvensen på 440 Hz, den der midten står i ro og de to halvdelene av strengen svinger i motfase er den første overtonen, og har en frekvens på 880 Hz i dette tilfellet.
Hvis vi gjør en frekvensanalyse av denne lydfilen kan vi finne ut mer om hvilke frekvenser signalet består av, og resultatet ser slik ut:
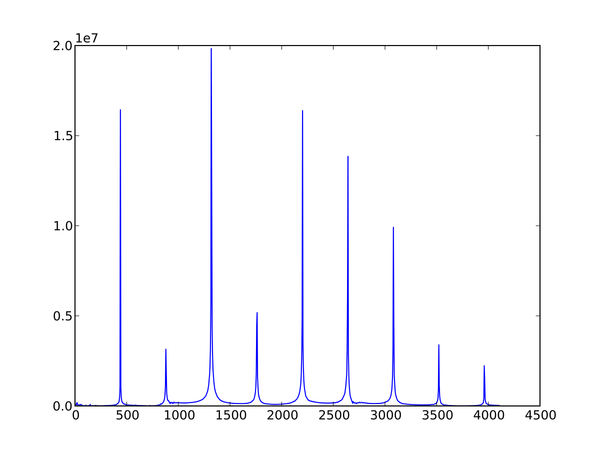
Denne frekvensanalysen har jeg funnet ved å gjøre noe som kalles å ta en Fouriertransform av signalet. Fouriertransformasjoner dukker opp både titt og ofte når man gjør beregninger i fysikk, og det å kunne regne dem ut raskt er derfor viktig. En rask algoritme for å regne ut en Fouriertransform kalles gjerne en Fast Fourier Transform (FFT), og det finnes en hel bråte av dem. Det som skiller disse algoritmene er at de bruker ulike typer triks for å få utregningen til å gå fort, og hvilket av disse triksene som er best henger ofte sammen med lengden på signalet man transformerer. Derfor var det et par smarte fyrer, Matteo Frigo og Steven G. Johnson, som skrev et bibliotek som analyserer problemet og velger den algoritmen som gir det beste resultatet. Siden dette biblioteket alltid velger den raskeste algoritmen kalte de det the Fastest Fourier Transform in the West, eller FFTW.
Og det er altså grunnen til at jeg kunne tenke meg en t-skjorte med teksten «FFTW FTW».
-Tor Nordam