Å sammenligne uendeligheter
Jeg snakket en jeg kjenner ved universitetet i Edinburgh her en dag, og han kunne fortelle at han nettopp hadde overbevist sin ti år gamle sønn om ikke alle uendeligheter er like store. Han hadde tatt utgangspunkt i de hele, positive tallene, og sagt til sin sønn at han kunne skrive opp alle oddetallene, mens han selv tok alle hele tall. Da var det vel åpenbart at han til slutt ville ha dobbelt så mange tall som sønnen, noe sønnen motvillig gikk med på.
Der og da tenkte jeg ikke så mye utover saken, utenom at det virket som en noenlunde oppvakt tiåring, men litt senere innså jeg at det ikke stemmer. Det vil si, alle uendeligheter er ikke like store, men de to i dette eksempelet er faktisk det. Ethvert positivt oddetall kan nemlig skrives på formen
som betyr at for ethvert positivt heltall finnes det et positivt oddetall. Altså er det like mange av dem. Funky, eller hur?
-Tor Nordam

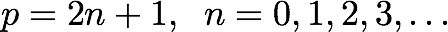
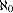 .
.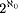 , stemmer ikke eksempelet jeg ga tidligere. Med eksempelet mitt vil man åpenbart bare konstruere rasjonale tall, og ikke en gang alle de rasjonale tallene. De rasjonale tallene er dessuten tellbare på samme måte som heltallene, hvis man finner på en tilstrekkelig funky mapping (hva heter mapping på norsk), og har dermed samme kardinaltall som heltallene.
, stemmer ikke eksempelet jeg ga tidligere. Med eksempelet mitt vil man åpenbart bare konstruere rasjonale tall, og ikke en gang alle de rasjonale tallene. De rasjonale tallene er dessuten tellbare på samme måte som heltallene, hvis man finner på en tilstrekkelig funky mapping (hva heter mapping på norsk), og har dermed samme kardinaltall som heltallene.
Comments