Det var en gang en mann som het Hermann Grassmann. Han var visst litt av en helt, i følge wikipedia. Jeg sakser fra
artikkelen om ham:
Hermann Günther Grassmann (April 15, 1809, Stettin (Szczecin) – September 26, 1877, Stettin) was a German polymath, renowned in his day as a linguist and now admired as a mathematician. He was also a physicist, neohumanist, general scholar, and publisher. His mathematical work was not recognized in his lifetime.
Videre står det at han bortimot egenhendig oppfant lineær algebra, men at ingen skjønte hva han drev med, så han begynte å sysle med lingvistikk i stedet. Det ante jeg faktisk ikke.
Det jeg derimot vet, er at han fant noe funky greier som heter Grassmann-tall, eller Grassmann-variable. Og det heller var det nok ikke så mange som brydde seg om på 1800-tallet, men på 19060-tallet, når folk begynte å sysle med kvantefeltteori på skikkelig vis, da var det en russer som het Berezin som fant frem tallene til Grassmann, og viste at de kunne brukes til ting.
Grassmann-tall har den funky egenskapen at de antikommuterer. Det vil si at hvis eta og theta er to Grassmann-tall, så har vi:
Fra dette kan vi slutte at produktet av et Grassmann-tall med seg selv må være null. Hvis ikke blir det bare tull.
Det har imidlertid også en interessant konsekvens. Grassmann følte at det var en viktig egenskap ved funksjoner av vanlige tall at de kan rekkeutvikles, og han så ingen grunn til at Grassmann-tallene skulle være annerledes. Men siden kvadratet av et Grassmann-tall er null, betyr det at den lengste rekkeutviklingen, og dermed den mest generelle funksjonen, av et Grassmann-tall er
der
a og
b er vanlige tall.Spennende, spennende. Videre følte Grassmann at det var en viktig egenskap ved ordinære integraler at man kunne skifte litt på integrasjonsvariabelen uten at det gjorde så mye. Spesifikt at man kunne gjøre slik:
Så dermed bestemmer vi at vi kan gjøre det samme med et integral over en funksjon av Grassmann-tall:
Og nå kommer vi til punktet der jeg begynner å stusse. Noen lærebøker slutter nemlig derfra til at
Det er jeg imidlertid ikke villig til å gå med på sånn helt uten videre. Det er for eksempel greit nok at
Men det er vel ingen som slutter derfra til at
Jeg mistenker imidlertid at
og videre
egentlig er en definisjon, heller enn noe man kan vise. Hvordan det fremstilles kommer imidlertid ganske mye an på hvilken lærebok man ser i. Nesten enda mer diffust argumenteres det imidlertid for
Der sier man gjerne noe slikt som at produktet av to Grassmann-tall er et vanlig tall, noe man kan se fra
føler man at et Grassmann-tall integrert med hensyn på seg selv bør være et vanlig tall, så hvorfor ikke 1?
Såh. Grunnen til at jeg tenker på dette akkurat nå, i stedet for på solceller og/eller fortran, er at det nærmer seg eksamen i et av fagene jeg tar, og det faget handler om slikt som dette. Når jeg er ferdig med denne eksamenen har jeg tatt to av fagene jeg trenger i doktorgraden, så da mangler jeg fortsatt to. Dette kan med andre ord bli min tredje siste eksamen noensinne. Ikke verst, ikke verst.
I morgen: Verdens mest hypede supermagnet.
-Tor Nordam


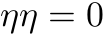
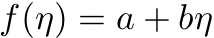
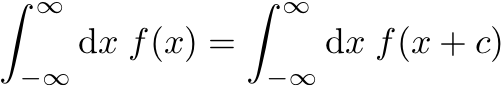
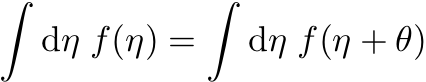
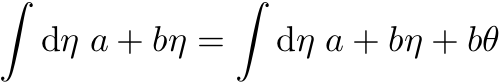
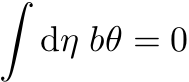
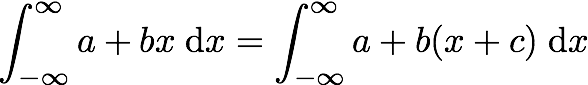
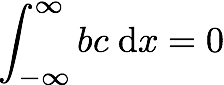
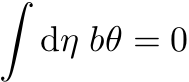
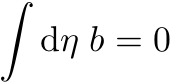
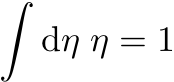
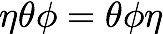
Comments