I dag satte jeg meg ned for å ferdigstille den siste øvingsoppgaven i faget mitt. Alt som mangler er en bonusoppgave, og inspirert av dagens forelesning, som var om gravitasjonsloven, og en diskusjon med Paul Anton, kom jeg frem til at å regne ut posisjonen til Lagrangepunktene i Sol-Jord-systemet måtte være en passende utfordring. Og sånn ca her er det antagelig på sin plass med en forklaring på hva Lagrangepunktene er.
Det har seg slik at når en gjenstand går i sirkelbane rundt Solen er omløpstiden, altså tiden gjenstanden bruker på en runde rundt Solen, entydig bestemt av baneradien, altså avstanden fra Solen. Dette skyldes at tyngdekraften som virker på gjenstanden er avhengig av avstanden, og hvis jeg kan tillate meg å bruke et litt upresist uttrykk må da farten være så stor at sentrifugalkraften nøyaktig opphever tyngdekraften. Og det bestemmer farten. Eller, for å si det mer presist:
der
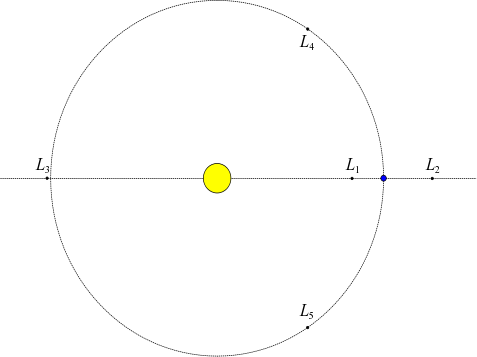
M er massen til Solen. Det betyr at hvis en gjenstand skal ha samme omløpstid som Jorden er den pent nødt til å befinne seg i samme avstand fra Solen. Problemet er imidlertid at Jorden, med sine 6 millioner milliarder milliarder kilo (Fakta. Det er det som er massen til Jorden) slett ikke er noen lettvekter, og vil trekke til seg eventuelle andre ting som prøver å dele bane med den. Det viser seg likevel at det finnes 5 punkter der en gjenstand kan gå i bane rundt Solen, med samme omløpstid som Jorden, og disse fem punktene kalles Lagrangepunktene.
Det første Lagrangepunktet, L
1, ligger mellom Jorden og Solen, i den avstanden som er slik at tyngdekraften fra solen, minus tyngdekraften fra Jorden (fordi den peker i motsatt retning) er nøyaktig nok til å motvirke sentrifugalkraften. Vel, tenkte jeg, det må da vel være en smal sak å regne ut. Så jeg gjorde som jeg vanligvis gjør når jeg ser på problemer som er en smal sak å regne ut. Jeg slo opp på wikipedia. Artikkelen om
Lagrange punktene viste seg imidlertid å være skuffende fri for matematiske uttrykk. Nuvel, tenkte jeg, og gikk til plan B, som var å regne ut skiten selv.
Jeg skrev ned noen uttrykk, forenklet og herjet litt, og endte opp med
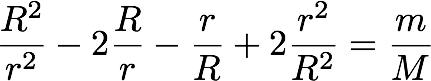
Med andre ord en fjerdegradsligning. Typisk. Nuvel, tenkte jeg, det er vel ikke verre enn å spørre Mathematica. Og, som sagt så gjort, og Mathematica hadde naturligvis et svar. Dessverre tok svaret uhåndterlige fem skjermbilder i terminalen. Jeg er litt bitter, da jeg synes det virket som en god oppgave, men når svaret blir såpass komplisert tror jeg det kommer litt i veien for forståelsen av problemet.
Jeg kan ellers nevne at det finnes en forening ved navn
L5-Society, som tilsynelatende støtter opprettelse av en permanent romstasjon i L
5. Hva de har imot L
4 vites ikke, men stridigheter mellom Lagrangepunkter er ikke et helt ukjent tema. I Lagrangepunktene til Jupiter befinner det seg en samling astroider, og de i L
4 kalles «Greeks», mens de i L
5 kalles «Trojans».
-Tor Nordam

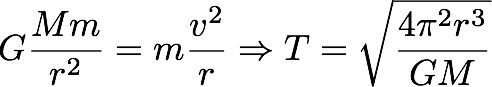
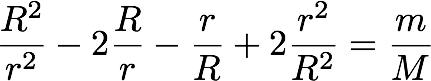
Comments