Jommen greide jeg ikke å finne drafts jeg også, etter å ha tenkt meg om litt. Ikke værst?
Ellers tenkte jeg at jeg skulle kjøre på med en figur til oppgaven fra i går. Her er den:
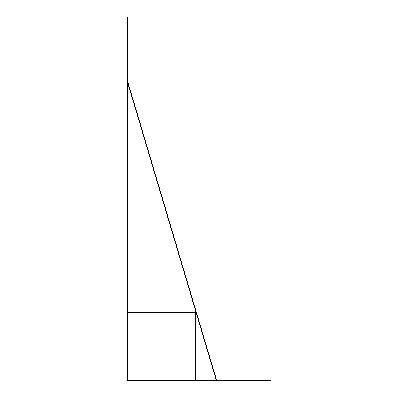
Denne burde illustrere tydelig hvilke to løsninger jeg tenkte på, nemlig den som er på figuren, og den man får ved å tippe figuren på siden, slik at vegg blir gulv, ogsåvidere.
Ellers har jeg et bilde til, det er et bildet av taket mitt, tatt med blender 16 og lukkertid 3 sekunder eller noe slikt. Akkurat det er ikke så viktig. Det som er viktig er hva bildet kan fortelle oss.

Det forteller i allefall meg at det er på høy tid å investere i SensorSwabs(tm). For de som kanskje tenker at jeg også burde vurdere noen CeilingSwabs(tm) kan jeg avsløre at ingen av de stygge, svarte flekkene på bildet stammer fra taket mitt.
Kanskje Eivind har noe å anbefale her, det var jo han som solgte meg skiten.
Til slutt vil jeg henlede alles oppmerksomhet på en liten sak som angår oss som bloggere. Som vi vet er det jo Google som eier dette bruket her, og det stod noe om dem på
dagbla'.no i dag. Det stod rett og slett om en mann som jobbet for Google, som fikk fyken fordi han kritiserte jobben i en
blogg, nettopp på blogspot.com. Men som vi ser fikk han beholde bloggen, og siden ingen av oss jobber for Google er det vel ikke noe å bekymre seg så veldig for.
-Tor Nordam



Comments