Her en dag bestemte jeg meg for å regne ut Christoffelsymbolene i polarkoordinater i flatt rom. Det var ikke akkurat «et øyeblikks opplysning» eller noe slikt, og det hadde jo egentlig vært mye kulere, men jeg bestemte meg i alle fall. Riktignok hadde veilederen min sagt at jeg burde regne ut Ricci-skalaren i polarkoordinater i flatt rom, fordi «det er ganske lærerikt, og vil neppe ville ta mer enn et par dager», og da er Christoffelsymbolene et naturlig første skritt, men det var jeg til syvende og sist jeg som bestemt at jeg ville gjøre det.
Som vi vet er firervektorer gitt ved
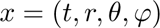
den aktuelle metrikken er

og uttrykket for Christoffelsymbolene er
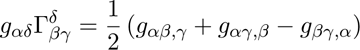
(Bak hver
g står det tre indekser. De to første henviser til en komponent i metrikken, for eksempel er 00 den som er øverst til venstre, 03 er nederst til venstre og 33 er nederst til høyre. Den indeksen som står bok kommaet indikerer at det skal deriveres med hensyn på den aktuelle komponenten av
x, som også er nummerert fra 0 til 3.)
Så da er det egentlig bare å sette i gang. Det første vi kan merke oss er at av de 64 mulige kombinasjonene av indekser kan vi raskt se at en hel del av dem må være null. De 24 kombinasjonene med tre ulike indekser må være null, ettersom alle kompontentene i metrikken som ikke ligger på diagonalen er null. Av de Christoffelsymbolene som har to like indekser må åpenbart de med 00 og 11 være null, ettersom 00- og 11-komponentene i metrikken er konstanter, så der har vi 16 til som er null. Til slutt ser vi at de eneste som blir forskjellige fra null er de som inneholder kombinasjonene 221, 331 og 332, da 22-komponenten av
g kun avhenger av
x1, og 33 kun avhenger av
x1 og
x2. Vi har altså ni Christoffelsymboler som er forskjellig fra null.
Setter man inn og regner ut kommer man frem til følgende resultat.
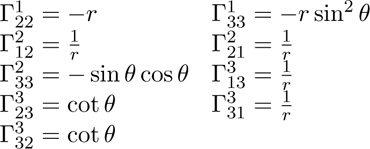
Så hvorfor poster jeg dette her? Vel, jeg skulle gjerne sjekket om jeg har kommet frem til riktig svar, men jeg greide ikke å finne disse noe sted på nettet. Derfor poster jeg her, og håper på at minst en av våre lesere har både de nødvendige skills og en tilstrekkelig pedantisk legning til å si fra om noe er feil. Og hvis det er riktig vil jeg jo si at jeg gjør menneskeheten en tjeneste ved å gjøre resultatet tilgjengelig for alle og enhver.
-Tor Nordam

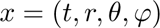

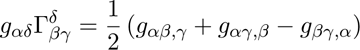
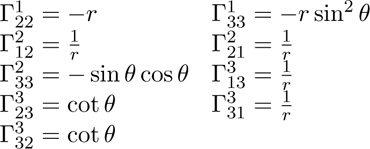
Comments